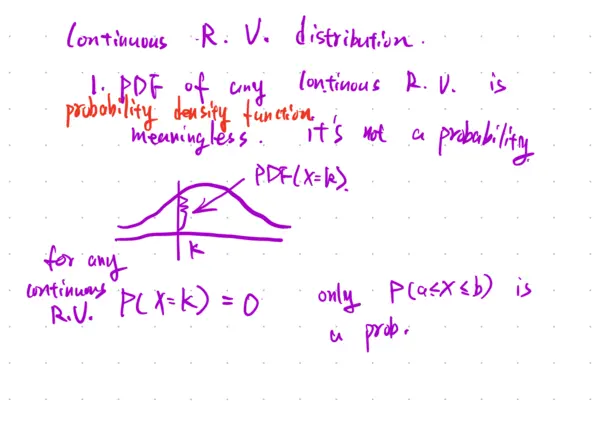
Continuous R. V. distribution. 1. PDF of any continuous R. V. is probability density function meaningless. it's not a probability PDF(X=k). for any continuous R.V. P(X=k) = 0 only P(a<=X<=b) is a prob. 2. P(a<=X<=b) => CDF Cumulative distribution function For discrete R.V. PDF is prob. i.e. P(X=k)>0 For continuous R.V. PDF is not probability. P(X=k) = 0. Special continuous R.V. distribution. 1) uniform distribution X ~ Uniform (a, b) Area=1 symmetric E(X)=Med(X). a b a P(i<=X<=j) = (j-i)/(b-a). E(X)= (a+b)/2. std(X)= (b-a)/sqrt(12). 2) normal distribution X ~ Norm (mu_x, sigma_x) bell-shaped density curve symmetric P(a<=X<=b) = normalcdf (lower: a, upper: b, mu: mu_x, sigma: sigma_x) mu, sigma is a given parameter. one R.V. E(X +/- a) = E(X) +/- a. E(kX)= kE(X). E(kX +/- a) = kE(X) +/- a. Two R.V. E(X +/- Y) = E(X) +/- E(Y). no condition. E(aX +/- bY +/- c)= aE(X) +/- bE(Y) +/- c. E(aX + bY + cZ + d) = E(X) +/- bE(Y) +/- cE(8) +/- sqrt. std (aX) = |a| Std(X). Std (X+b)= Std(X) Std (aX+b) = |a| Std(X). std (X +/- Y) = sqrt(Std^2(X) + Std^2(Y)) std(X +/- Y +/- Z) = sqrt(Std^2(X) + Std^2(Y) + Std^2(Z)) Std (aX + bY + c) = sqrt(a Std^2(X) + b Std^2(Y))